[Research] 实时可交互沙土模拟方法 - 物理部分

本篇介绍一种移动端实时交互式沙土模拟方法

Real-time Interactive Sand Simulation in Mobile Platform

背景/Background

移动端抽卡玩法已经屡见不鲜，表现形式多为点击、播片，玩家在一次次重复的交互过程中多多少少会产生疲倦感，于是我们决定在玩家交互上下点功夫，带来一些新鲜感。玩法设计上，我们希望是移动端二维俯视角，玩家通过交互刷开覆盖的沙土，发现新的收集品，让玩家在交互过程中体验小心翼翼的紧张感与仪式感，增加开奖时的快乐。

技术挑战/Challenge

首先明确一下我们的效果目标：二维俯视角下的可交互沙土模拟，沙子渲染要有真实感，物理模拟要有体积感。玩家刷开沙子的过程中，沙子的运动要符合真实物理规律，能够被推开，也能够堆叠。当然最主要的是，在移动端，速度要快！

确定技术方案之前，先来看看现实世界里的沙子是怎么组成的。
沙子的成分因产地而异，但其主要还是由矿物和微小的岩石碎片组成。岩石碎片是岩石经过侵蚀和风化而成，颗粒微小，这使得沙子的物理特性有点像流体，但又不能完全套用流体力学的计算方式来模拟其运动过程。

我们先来看看市面上现有的游戏，下图是在沙子模拟效果上比较有代表性的两款作品，但它们明显在模拟规模上偏大，而且在体验上更注重于渲染效果，而非玩家交互，所以无法满足我们的需求。

这两种模拟方法对于现在的新需求来说，都是不适用的，主要原因有以下两点：
1、上面两款游戏的方法适用于沙漠场景中的大规模流沙模拟，是对沙子运动的一种宏观描述，而我们仅需要一小堆沙子；
2、我们希望沙子是能够在有限的交互次数内被刷干净的，而不是永远“流”不完的。

要实现以上这些目标，就必须要有一个相对更加“物理”的模拟方法。图形学上实现真实沙子物理模拟的方法有很多，比如下图是基于物质点法（Material Point Method，MPM）使用Taichi实现的沙子物理模拟：

MPM是一种将欧拉法（Eulerian）和拉格朗日法（Lagrangian）结合起来的计算方法，既避免了欧拉法要求解对流项的难题，又解决了拉格朗日法在处理大变形时的网格畸变和负体积问题，主要用于求解冲击、爆炸等高速、大变形问题，尤其是在沙子的动力学解算中非常常用。

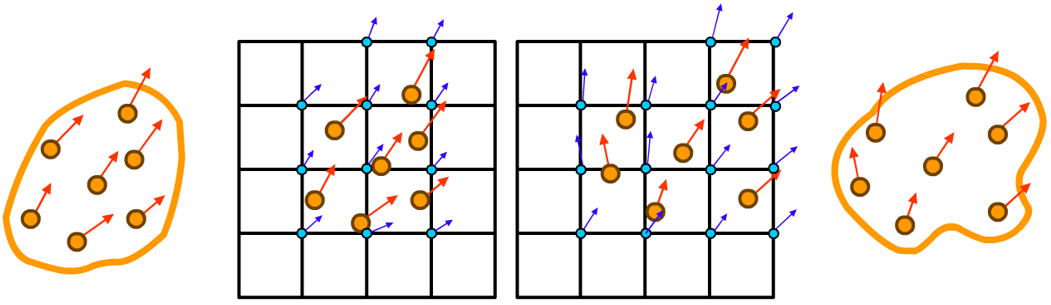
MPM中，沙粒的各种信息被保存在一个个离散的物质点上，然后：
1、将物质点上的信息通过形函数 (Shape Function)映射到背景网格的节点上（Point to Grid，P2G）；
2、通过传统的有限元法（Finite Element Method，FEM），计算单元刚度矩阵、荷载列阵，加入边界条件，求解节点位移、速度等信息；
3、求解完后再通过Shape Function将单元节点上求解出来的信息映射回物质点上（更新物质点的位置、速度等；G2P，Grid to Point）；
4、删除背景网格，返回第1步循环迭代。

MPM作为欧拉法和拉格朗日法之间的媒介，巧妙地在综合两种方法优点的同时又避免了两种方法自身的缺点，能够很好地模拟沙子的流动、扩散、堆叠现象，但它有个致命的问题，就是在移动端——会遇到性能瓶颈。
这时我们会很自然地想到：既然是固定视角，直接做2D MPM效率会不会好呢？现实比较残酷，即使是2D MPM，在移动端单独跑沙子交互都依然帧率堪忧，就别提场景里还要加其他东西了。

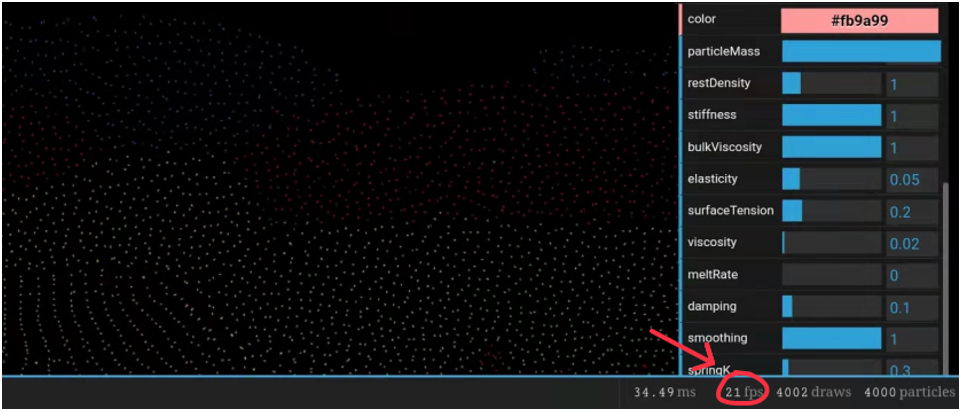
再看看shadertoy和youtube上大佬们基于其他解决方案的2D沙子模拟案例，都无一例外是正视图，没有俯视图的案例。而且模拟中直接丢弃了深度信息，沙子没有体积感，物理效果和渲染效果都不够写实。

于是至此我们可以得出结论：现有方案里没有能够满足我们需求的，我们需要一个切实可行的新方案，且主要挑战在于要在满足效果需求的前提下做到在移动端落地。但究竟能不能找到这样一种方法以及能不能顺利落地，我们心里也没底，所以计划是先预研一版看看能否满足我们的效果目标，如果不行，就用简陋一些的“擦玻璃”方案作为保底。

模拟部分/Simulation Part

Ubisoft曾在SIGGRAPH 2020上发过一篇Paper：

这篇Paper通过离线预计算的可分离泊松滤波器（Separable Poisson Filter）将基于欧拉法的流体模拟降维投影到纹理空间，在模拟质量几乎不变的情况下，实现了大幅性能提升：

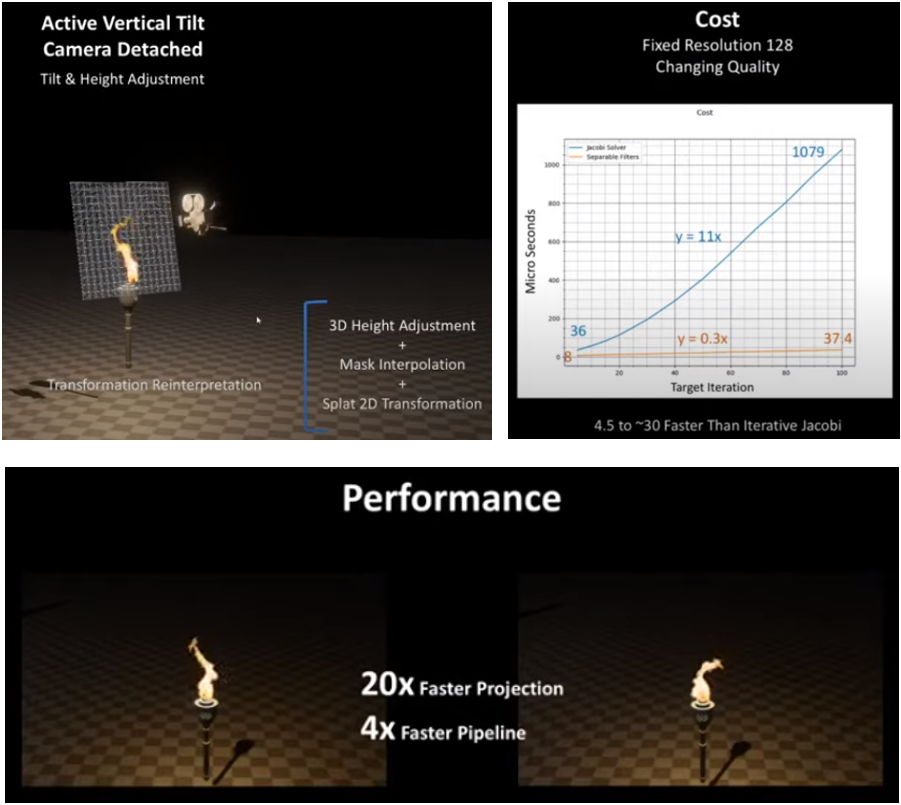
受其启发，沙子的物理模拟实际上也可以做降维与并行化的优化！由于是俯视角模拟，摄影机是不动的，所以首先我们可以把三维世界空间下的沙粒压缩到一张RGBA纹理上，x和z轴对应纹理空间u和v轴，y轴则压缩到纹理深度，这样就不会丢失沙堆的厚度信息。而且，当我们使用分辨率足够高的纹理进行采样的时候，实际上可以近似地把一个像素点看作一粒沙子：

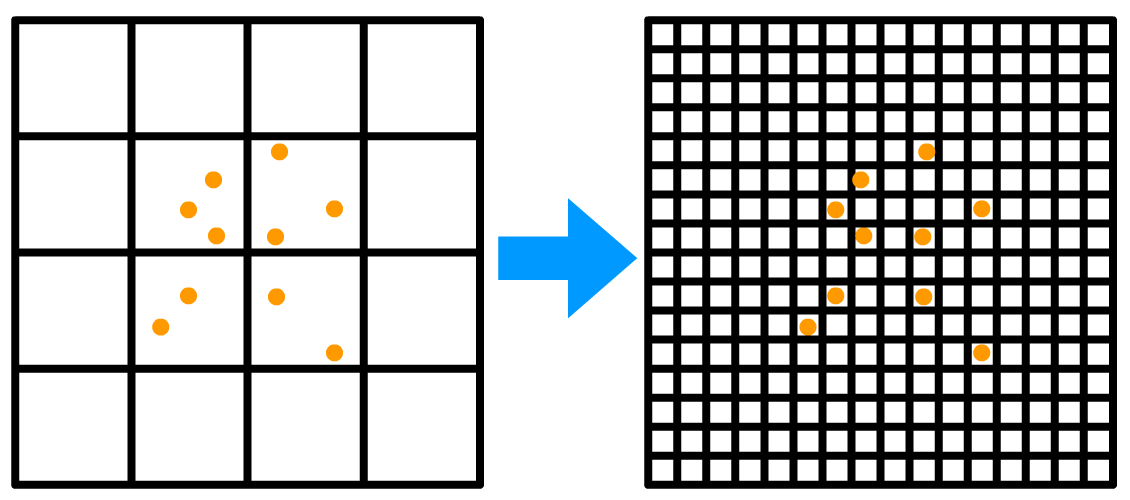
于是我们就不再需要做MPM中P2G和G2P的过程，直接基于像素点模拟即可。
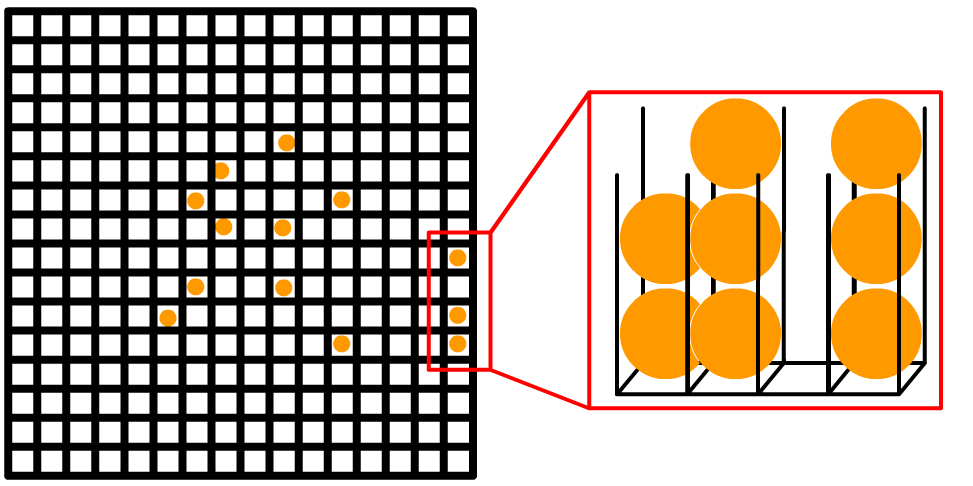
但需要注意的是为了模拟沙子的堆叠，让沙堆在交互过程中更有体积感，我们需要额外维护一个深度通道。由于降维后我们的网格是二维的，因此实际上这就像一个格子里面摞了一叠“小球”，而不是像MPM一样是一个三维网格，每一个网格里平铺多个小球！

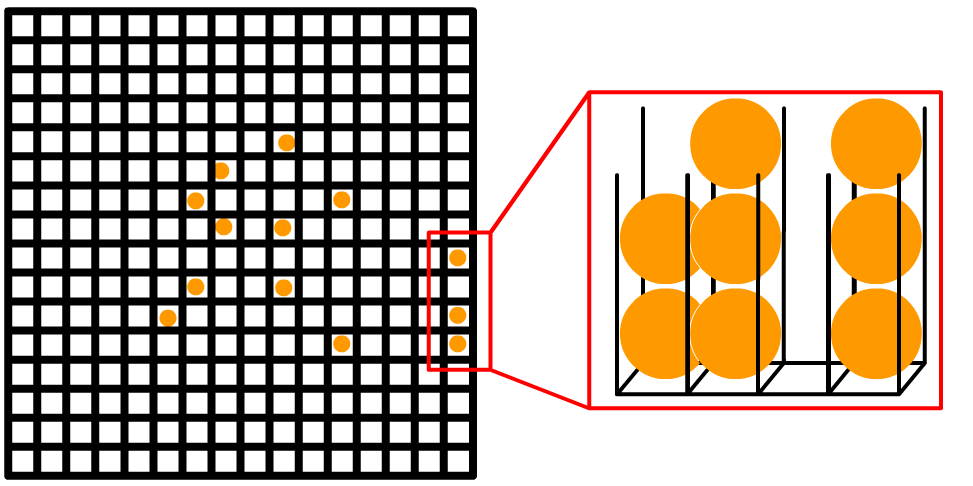
这个模拟方法我们就称之为DRSS（Dimension Reduction Sand Simulation），整个模拟流程就像这样：

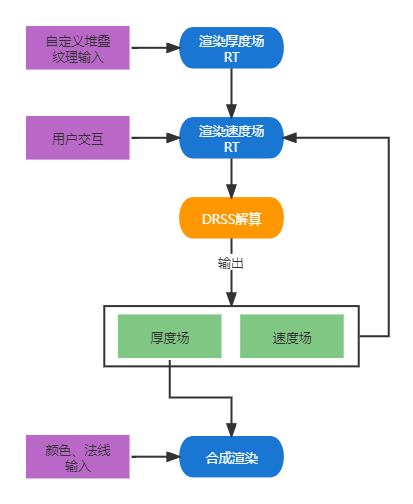
1 - Preparing Thickness Buffer

首先需要准备一个Thickness Buffer，就像这样：

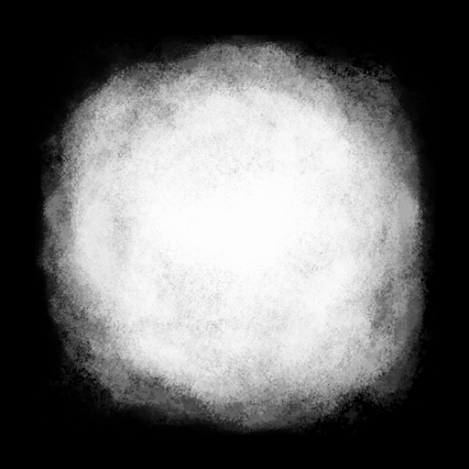
我们之前提到过，DRSS的模拟是带有深度信息的，Thickness Buffer就用于模拟沙堆的厚度（深度）。Thickness Buffer并不是程序化生成的，而是手动绘制的，实际模拟中，我们使用纹理的A通道来作为深度通道。用A通道作为Thickness Buffer的好处是，模拟完成之后，在着色阶段，我们可以直接将深度通道作为沙堆的Alpha值来进行渲染，无需进行其他的转换。
而Thickness Buffer之所以要手动绘制，是为了方便artist在使用这套模拟系统的时候，能够方便地指定想要的沙堆的形状和厚度，Thickness Buffer可以简单地基于PS的干介质笔刷绘制得到。

2 - Rendering Velocity Buffer

然后需要准备一个Velocity Buffer，像这样：

Velocity Buffer的作用是描述每一个像素点位置沙子的运动方向，由于俯视角下不需要考虑重力，沙子在无交互情况下是静态的，所以实际上速度场只需要包含玩家交互部分的速度向量就可以了。
速度向量可以是世界空间下的也可以是转到屏幕空间下的，但注意如果用世界空间速度，输出时不能对速度向量做clamp。

3 - DRSS Solver

3 - 1 - 流动分量（Flow Component）

对沙子“流动”分量的描述，DRSS中使用半拉格朗日法（Semi-Lagrangian）实现：

$p' = p - dt*vp$

即对于每个位置p，根据位置p的速度v_p，反向寻找到位置p’，使用位置p’ 的场的值来作为位置p的新场值。然后不断迭代，以此来描述沙子的运动：

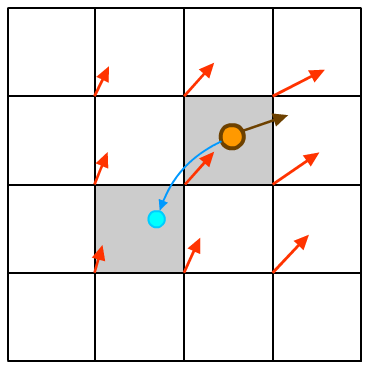
但由于我们要并行化地解算沙子的运动，所以不能直接使用上式求解，而是要将其改写成一个类似联合双边滤波（joint bilateral filter）的3x3卷积核形式来使用：

${F_{Kernel}} = V \cdot \left[ {\begin{array}{ccccccccccccccc}1&1&1\\1&0&1\\1&1&1\end{array}} \right]$

其中V为速度场。于是可得：

$P' = P - dt*{F_{Kernel}}$

其中P’和P为位置矩阵。于是我们就可以得到沙子运动的流动分量，下图为不同速度下的流动分量模拟结果，交互物体从右侧开始运动，红线为停止线。可以看到速度较慢的时候，沙子运动距离短；速度快时，沙子运动距离更长，模拟结果符合物理规律。

3 - 2 - 扩散分量（Spread Component）

由于沙子互相之间会发生碰撞挤压，因此除了单纯的流动之外，随着交互物体的移动，沙子还会在运动过程中发生扩散。
扩散分量我们使用下式描述：

$S = Lq \cdot {\rm{D}}({\rm{Dot}}(p - q,{\hat v_q}),\theta )$

其中，p和q分别为当前像素点坐标和邻域像素点坐标；L_q为衰减因子，我们在下一部分堆叠分量中作详细介绍；Dot(a,b)为求向量a和b的点积；${\hat v_q}$为规范化后的速度场在位置q处的速度向量；θ为扩散角度，由用户指定。

D(x,θ)为扩散函数，它是一个分段函数：

${\rm{D}}(x,\theta ) = \left\{ {\begin{array}{ccccccccccccccc}{1,x > \theta }\\{0,otherwise}\end{array}} \right.$

扩散分量的模拟结果见下图，θ越大，随着交互物体的运动沙子会在流动的过程中扩散地越远；而当θ越接近0，则沙子只会在直线上流动。

3 - 3 - 堆叠&迁移分量（Drift Component）

虽然是降维模拟，但我们希望沙堆能具有体积感，单纯地基于像素点模拟单层沙子是无法体现出体积感的，因此堆叠分量就是基于我们最初设计的存储在A通道中的Thickness Buffer模拟厚度不匀的沙堆的体积感。

我们可以把厚度的模拟看作这样一个过程：每一个像素点上垂直堆叠了多层沙粒，每一次玩家交互，交互物体略过沙堆表面时，我们限制让其只能带动一定层数的沙粒，并且被带动的沙粒能够通过流动和扩散转移到其他像素格里，这样一来，就能够模拟沙堆的体积感了。

实际迭代中，我们用下式描述这一过程：

$Drift = \sum\limits_{q \in S} {Lq \cdot {\rm{D}}(A,\theta ) \cdot {F_{Kernel}} \cdot Tq}$

$A = {\rm{Dot}}(p - q,{\hat v_q})$

其中${T_q}$为像素p邻域S内的任意点q处的厚度值；衰减因子${L_q}$由两个分量组成：

$Lq = {{\rm{G}}_{\sigma S}}(||p - q||) \cdot {\rm{L}}({T_p})$

第一个分量G为高斯核，用于限制堆叠分量在向周围像素转移过程中的移动距离；第二个分量为一个分段函数L(x)：

${\rm{L}}(x) = \left\{ {\begin{array}{ccccccccccccccc}{loss,x \ge 0.5}\\{1.0,otherwise}\end{array}} \right.$

loss是损失常量，由用户指定。loss为1.0时，沙子在转移过程中不会产生任何厚度损失，完全物理正确，但实际体验会发现这种情况下玩家需要反复擦拭一个位置才能把这个位置的沙子完全清理干净，看到下面覆盖的东西，玩起来很累，玩家体验不好。因此增加loss常量就能够让沙子在转移的过程中不断产生微小的厚度损失，让沙子更容易被擦干净：

4 - Bring all the components together!